Programmer 
Content
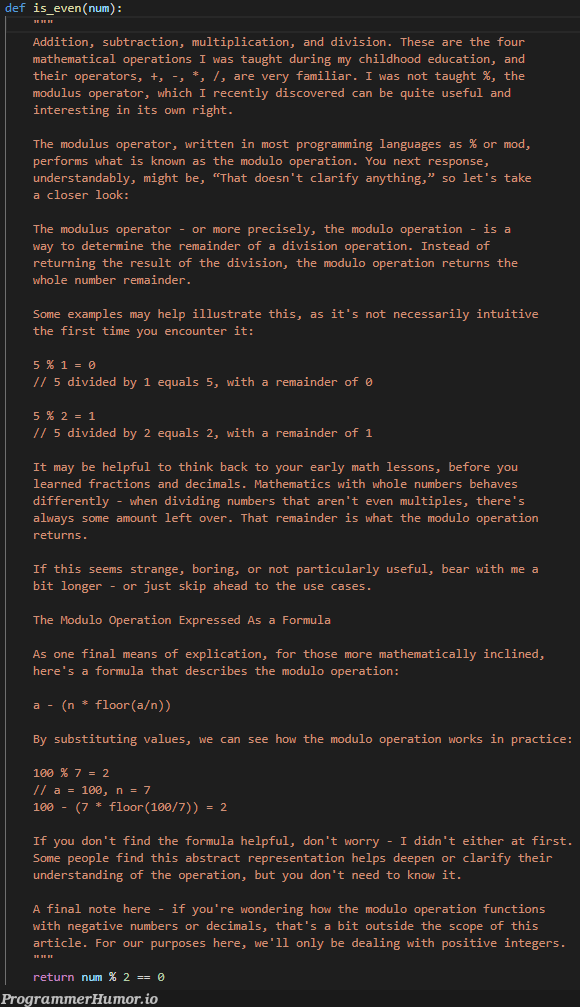
det ic even (num: Addition, subtraction, multiplication, and division. These are the four mathematical operations I was taught during my childhood education, and their operators, t; , are very familiar. I was not taught , the modulus operator, which I recently discovered can be quite useful and interesting in its own right. The modulus operator, written in most programming languages as or mod, performs what is known as the modulo operation. You next response, understandably, might be, "That doesn’t clarify anything," so let’s take a closer look: The modulus operator – or more precisely, the modulo operation – is a way to determine the remainder of a division operation. Instead of returning the result of the division, the modulo operation returns the whole number remainder. Some examples may help illustrate this, as it’s not necessarily intuitive the first time you encounter it: 5 1 0 5 divided by 1 equals 5, with a remainder of 0 5 2 1 5 divided by 2 equals 2, with a remainder of 1 It may be helpful to think back to your early math lessons, before you learned fractions and decimals. Mathematics with whole numbers behaves differently – when dividing numbers that aren’t even multiples, there’s always some amount left over. That remainder is what the modulo operation returns. If this seems strange, boring, or not particularly useful, bear with me a bit longer – or just skip ahead to the use cases. The Modulo Operation Expressed As a Formula As one final means of explication, for those more mathematically inclined, here’s a formula that describes the modulo operation: a – (n floor (an)) By substituting values, we can see how the modulo operation works in practice: 100 7 2 100, n 7 100 – (7 floor (1007)) 2 If you don’t find the formula helpful, don’t worry – I didn’t either at first Some people find this abstract representation helps deepen or clarify their understanding of the operation, but you don’t need to know it A final note here – if you’re wondering how the modulo operation functions with negative numbers or decimals, that’s a bit outside the scope of this article. For our purposes here, we’ll only be dealing with positive integers. return num 2